Fractions
Partitioning and the part-whole concept
JONATHAN FISHER
KEY POINTS
•&&Students need to be exposed to a range of fraction ideas and representations in order to fully understand the difficult concept of “fraction”.
•&&Students who only work with, for example, circles divided into even-sized pieces, may develop limited strategies, such as counting the number of pieces rather than assessing the relationship of the part(s) to the whole.
•&&Results of ARB item piloting showed that some students did not understand that the whole must be divided into evenly sized pieces, and some students had difficulty when asked to partition unfamiliar shapes. Some students also did not understand that fractions can represent more than one whole or had difficulty when presented with problems where the “whole” was more than one object.
•&&Challenging these ideas—for example, by posing questions about various shapes partitioned irregularly—can help expand and deepen student thinking.
Fractions are known to be difficult. Jonathan Fisher explores why this is so, looking in particular at the crucial foundation concepts of part-whole relationships and partitioning. He outlines common student errors uncovered in piloting Assessment Resource Bank (ARB) items about fractions, and suggests some ways to help students gain a fuller understanding.
There are many important concepts within the realm of fractions and fractional thinking. This article aims to explore two of these important concepts: partitioning and the part-whole nature of fractions. These fraction concepts will be illustrated using items from the Assessment Resource Banks (ARBs)1 that were designed to explore students’ understandings and provide information to support next learning steps. Some common misconceptions that students develop around fractions showed up clearly in the classroom piloting and triallings of these items with a range of Year 4 to Year 8 students. These illustrate some of the underlying difficulties that fractions carry with them. Both partitioning and the part-whole concept are fundamental to learning about and understanding the nature of fractions.
To be able to confidently solve the diverse range of fraction problems, students need to develop an understanding of fractions rather than a procedure to solve particular problems. Many of the fraction problems in textbooks, websites and the various other sources of maths problems for students address the part-whole concept of fractions. The part-whole concept of fractions involves comparing the part (or parts) with the total number of parts that make that whole. However, there are also a range of other types of fraction problems: finding a fraction of an amount (set, or region), using fractions as operations, fractions as division relationships, using fractions as measures, adding and subtracting fractions, multiplying and dividing fractions, comparing fractions, ordering fractions, marking fractions on number lines, re-unitising fractions and fraction problems involving partitioning. Many of these concepts are described in the fractional thinking concept map2 on the ARB website.
Mathematics achievement objectives in The New Zealand Curriculum (Ministry of Education, 2007) indicate that students are expected to make sense of most of these concepts, types and representations. Students who have only experienced limited types of fraction problems (for example, only part-whole concept problems) may not be able to even understand what is being asked when presented with other types of problems.
In addition to these concepts, there are different types of fractions: unit, non-unit, proper and improper fractions. There are also many ways to represent a fraction (for example, as a shaded region, a set, a mark on a number line or a rational number). Not surprisingly, students who have only been exposed to limited representations of fractions (for example, only shaded regions) may well develop insufficient strategies for solving other fraction problems.
In this article the ideas about teaching and learning fractions are based on the assumption that learning involves developing understanding rather than a veneer of knowledge (without the why or how), and that this understanding supports students to make connections between maths problems and to be able to transfer solving strategies to other similar problems.
Fractions: Complex and rich
Fractions are known to be difficult. NEMP results (Flockton, Crooks, Smith, & Smith, 2006) indicate some of the areas where students have difficulty with fractions; for example, fractions on number lines, improper fractions and performing arithmetic operations with fractions. Recent ARB item trialling results indicate that many students find items involving fractions hard— particularly items that require a deeper understanding. A considerable body of research concurs that fractions are complicated, difficult or at least strange (Anthony & Walshaw, 2007; Moss & Case, 1999; Newstead & Murray, 1998; Young-Loveridge, Taylor, Hāwera, & Sharma, 2007).
So why are fractions difficult? One common reason is that students may only be aware of natural numbers (counting numbers) and have not realised that shared parts can be described numerically. Another reason is that they “inappropriately apply whole number ideas” (Lamon, 1999, p. 67). Some of the rules from natural numbers can be used directly, but some cannot: for example, multiplying for fractions and whole numbers is very similar, whereas adding is not. Fractions may also be hard because solving fraction questions can require multiplicative reasoning (Anthony & Walshaw, 2007; Lamon, 1999; Vanhile & Baroody, 2002). Another reason may be that some of the different types of fraction questions do not connect to students’ prior internalised learning, and therefore students have not developed a strategy to understand the question (Mack, 1990). This may relate to students “doing fractions” by performing steps (Lamon, 1999; Mack, 1990). Fractions also look funny. There seem to be two numbers in some kind of relationship. For example, the fraction 20/11 is a rational number with a value of about two. But it has the component numbers 20 and 11, which are each considerably more than two.
However, the complexities of learning about fractions also offer the potential for exploration into students’ solving strategies for new and complex concepts and can reveal some rich insights into students’ understandings:
No area of elementary school mathematics is as mathematically rich, cognitively complicated and different to teach as fractions, ratios and proportions. (Smith, 2002, p. 3)
Perhaps fractions are so rich because of the many concepts within the realm of fractions. Understanding fractions has been identified as an important gateway to later understanding of concepts in algebra, measurement and proportions (Behr, Lesh, Post, & Silver, 1983; Lamon, 1999; van de Walle, 2004, as cited in Young-Loveridge et al., 2007), and is, therefore, an important concept to grapple with.
Fractions have different personalities
As stated earlier, many current maths questions about fractions are about fractions as representations of part-whole concepts—either as sets, shapes or quantities. However, the part-whole concept is just one of the many flavours of fractions. Kieren (1993) identified four subconstructs that represent these conceptual “personalities” of fractions: fractions as division relationships (quotients); fractions as operators (performing an operation on a set, shape or quantity); fractions as measures;3 and fractions as ratios (part-to-part relationships). Many of these constructs develop the understanding that a fraction can also represent a single number (rational number) and has a value. The complexity of these constructs and the interrelation between them is another reason why students may find fractions confusing.
Students who may have developed an understanding that fractions represent some part of a whole (region, set or a quantity) and can identify and name that part are likely to come across fraction problems for which that knowledge is insufficient. All these different personalities need to be explored to develop students’ understanding of fraction sense (Kieren, 1995; Lamon, 1999; Young-Loveridge et al., 2007).
Partitioning
What partitioning and why?
Partitioning involves dividing an object, set of objects or number into parts. Knowing that shapes, sets and quantities can be partitioned into equal-sized parts, and understanding the importance of equal-sized partitions, is fundamental to recognising the part-whole relationship between the numerator and denominator in fractions:
Fundamental to the part/whole fraction sub-construct is the notion of partitioning a whole, whatever its representation, into a number of equal parts and composing and recomposing (i.e., unitising and re-unitising) the equal parts to the initial whole. (Baturo, 2004, p. 96)
Partitioning may be seen as trivial for some questions, but it clearly illustrates how the denominator is constructed, and, if combined with simple counting of the denominator unit (1/n), can be a very powerful tool to support student understanding of how fractions can be constructed (Lamon, 1999); for example, 3/7 = 1/7 + 1/7 + 1/7 = (1 + 1 + 1) sevenths.
A body of research identifies partitioning as an important early step in the development of understanding fractions (Lamon, 1999; Pothier & Sawada, 1983; Smith, 2002). Baturo (2004) adds that “according to Kieren (1983) partitioning experiences may be as important to the development of rational number concepts as counting experiences are to the development of whole number concepts” (p. 96). Partitioning (when combined with counting strategies) is an important aspect of students learning fractions as an extension of their whole number understanding (Olive, 2001; Steffe, 2002).
Students’ partitioning
Younger students with limited experiences may rely on the methods of cutting up things they are familiar with. If they have only ever divided up “pizzas”, they may think that this is the only way to divide shapes up. Using other shapes (for example, square cakes or rectangular loaves) can challenge this experience of a limited range of iconic representations.
Pothier and Sawada (1983) identify these stages of early understanding of partitioning: sharing, halving, repeated halving; evenness (recognising that parts must be equal sized); and oddness (being able to partition a shape, set or amount into an odd number of partitions). Using these ideas, teachers can develop a range of partitioning exercises that involve:
1.&&halving of basic shapes, then halving multiple times to derive other parts (e.g., 1/2,1/4, 1/8)
2.&&partitioning a variety of shapes: squares, two squares, rectangles, circles, hexagons (which are easier to partition accurately than circles) etc.
3.&&partitioning shapes into a different number of pieces (e.g., 3, 5, 6, 7, 9 etc.).
One important aspect of partitioning is the reasoning that students employ to indicate how they know the partitions are equal sized, and how they could justify this to somebody else by drawing, showing or explaining. Students may need to fold or cut and overlay the pieces to illustrate their point. Another aspect is that of encouraging students to find multiple ways of partitioning the same shape into the same number of parts (Lamon, 1999).
Partitioning questions from the ARBs
Looking at the level 3 assessment item Sharing shapes (NM0142), the first question involves partitioning a square (equally) between three people and naming the fractional part that each would receive:
EXAMPLE:
Draw lines to show how to share this square equally between 3 people.

What fraction would each person get?________
One of the common errors that younger students (Year 4 more than Year 6) exhibited for this question was that they did not recognise the need for partitions to be of equal size, and they used an inappropriate strategy to partition. About one-fifth of students from the trial (N = 138) attempted to partition a square into three parts as if it were a circle (or a pizza):

Half of these students went on to correctly identify the fractional part as 1/3. This representation may indicate that the students have predominantly used certain shapes (circles) and have developed a picture of what 1/3 is, rather than being aware that this is only one of many representations of 1/3.
Similarly, when students were asked to partition a hexagon, about half attempted to use vertical or horizontal lines rather than recognising the rotational nature of the shape and partitioning accordingly:
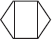
This was interesting as the hexagon was thought to be easier than a circle, as it aided students to use circular partitions without having to guess the angles, which are not explicitly identified until level 4 in The New Zealand Curriculum (Ministry of Education, 2007).
These examples highlight the importance of selecting appropriate shapes and shape-appropriate divisors (such as dividing a hexagon shape between three or six people) for their level, as well as using a variety of representations.
Another common error that students exhibited for partitioning a rectangular shape involved partitioning one more than the required number of parts. Here students may well be counting the lines rather than the number of parts, or have made a simple construction error. While there may be elements of geometric spatial awareness at play here, the concept of equal-sized parts for partitioning is fundamental for the naming system of fractions, as well as the construction of non-unit fractions from the unit parts.
Many of the errors above could be checked by asking students to explain their work to a peer or the teacher to identify if it is a geometric error or a conceptual error about fractions.
The last question in Sharing shapes (NM0142) explores partitioning of two shapes into a number of parts:
Draw lines to show how to share these
two squares equally between 5 people.

What fraction of a square would each person get?________
This type of question begins to explore what students do when the “whole” (or the unit) is not a single object. The idea that two objects may constitute a “whole” may be new to students who have previously only experienced partitioning whole numbers or single objects. Understanding what constitutes a “whole” (or the unit) is fundamental to developing an understanding of fractions (Baturo, 2004; Lamon, 1999).
Most of the students who partitioned the two squares in this question either partitioned each square into five equal parts:

or partitioned each square into two and a half (the centre “halves” join to form the fifth equal part):

The latter method makes it harder to identify the fractional value of “a square” because “a square” is not partitioned evenly, but it also indicates that students regard the two squares as the whole.
Under a quarter of students correctly answered that each person got 2/5 (of a square). A smaller number of students answered, 1/5 (of the squares). In this question students are asked “What part of a square would each person get?”, so the whole is a square, and the answer is 2/5. This understanding can become more blurred when talking about pizzas: how much pizza? how much of a pizza? how much of the pizza? The question “What is the whole (or unit) we are finding the part for?” could be one of the more vital questions that students and teachers could consider. Essentially, the important idea here is that students can identify the whole (unit) and the fraction being shared out to the number of people given. Through similar problems and discussion, students can explore how the two answers are different, and why they may be different. They may even begin to recognise that when the whole is two squares they get 1/5 and when it is one square they get 2/5, and that the fraction is twice as big when the referent whole (or unit) is half the size.
Students may also start to see the relationship between the number of squares and the number of pieces that both are divided into and see the division relationship between the numerator and denominator. In this way partitioning can also support students to develop an understanding of fractions as division relationships (quotients). In a level 4 ARB item, Partitioning pizza & fruit loaf (NM0168), students were asked to share four objects amongst five friends:
EXAMPLE:
Four fruit loaves were shared equally between 5 friends.

What fraction of fruit loaf did each person get?________
Many students recognised the division relationship and answered 4/5 of a loaf. Note that the question in this case was about the fraction of fruit loaf, so the whole was open to interpretation (and hopefully discussion about what constitutes the whole). Lamon (1999) notes that “research on partitioning has shown that greater economy in marking and cutting corresponds to more mature understanding of fractions” (p. 83). For the above question this could mean partitioning like:

rather than

Of course this means that to work out how much each person got, students would need to combine 1/2 + 1/5 (of a half) + 1/5, which is more complex than adding 1/5 four times.
Part-whole fractions
Although it is a commonly taught concept and a fundamental aspect of fraction learning, students still have difficulty with the part-whole concept of fractions (Chinnappan, 2005; Lamon, 1999). Understanding fractions as part-whole relationships involves recognising the relationship between the bottom number (total number of equal-sized parts that make up the whole) and the top number (number of these parts of interest).
Exploring part-whole fraction problems helps to develop the use of fractional notation. Part-whole concepts of fractions can involve regions (area), lengths (measurement), sets or quantities. Kieren (1993) identified the need for using fractions in a “variety of settings reflecting the various uses to which fractions might be put” (p. 38).
Most students’ first introduction to fractions in the classroom is as a part-whole comparison. This is usually first based on unit fractions, such as a half, a quarter or a third (1/2, 1/4 and 1/3). A unit fraction is one part of a whole. That whole may be partitioned into many parts, but as long as the fraction represents only one of these parts, it is called a unit fraction. For example, if a shape is partitioned equally into seven parts then each unit part is called one-seventh, and is written 1/7. Students who are exposed to only unit fractions may develop a strategy for solving or understanding that focuses only on the bottom number.
Most fractions are non-unit fractions. These are unit fractions that have been “numerated” or there is a count of more than one unit fraction; for example, 3/7 = 1/7 + 1/7 + 1/7. Students could then continue counting the unit fractions to make improper fractions (where the numerator is more than the denominator). For example, students could count … 5/7, 6/7, 7/7, 8/7 etc. Students who are exposed only to fractions less than one (proper fractions) may develop the belief that fractions are all proper fractions and find it difficult to reconcile, for example, how 8/7 can be a fraction. Additionally, students who are exposed only to common fractions with nice numbers (e.g., 1, 2, 3, 4, 5 etc.) may find it difficult to understand the range of numbers that fractions can be—in other words, that between any two fractions there are infinitely many fractions. For example, students may find it hard to understand that they can locate and name a fraction between 2/3 and 3/4 using a number line.
There are a significant number of part-whole fraction questions that can be solved by counting the parts and not recognising that those countable parts are a part of a whole. For example, questions like, “How much of this shape is shaded?”

Students can solve the problem by directly counting the part over the total number of parts without consideration to ensure equal size (because the shape is already partitioned evenly). Even with a derivation of this, such as  ,
,
students may answer 4/6 by counting the parts without any part-whole concept of fractions.
Questions that have irregular partitions are important to address students’ understanding about the importance of equal-sized parts in the naming of the fractional part. To explore students’ understandings about fractions as a part-whole relationship, a diagram of a quarter could look
like  or
or  .
.
In these examples students are required to work out the proportion of shading of the overall shape. This requires students to create their own parts to find the shaded fraction—indicating understanding of the need for equalsized parts as well as how to represent the shape using fraction notation.
The level 3 assessment item, Shaded fractions (NM0140), has a range of part-whole fraction questions about region. Some can be solved by counting and others require students to construct their own method for solving. Two of the shapes from this item are
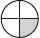 and
and  .
.
Students found the circle shape “very easy” and the square shape “moderate”. For the square, over a third of students answered 1/3. Yet both shaded portions are 1/4 of the whole shape.
Another level 3 assessment item, Shaded fractions (NM0144), is about working out how much of a shape has been shaded:
What fraction of the rectangle is shaded?
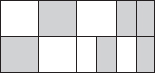
The parts that the shape has been broken into are irregular (not all the same size and not a multiple of the partition). This encourages students to start thinking about how much of the whole shape (a rectangle) is shaded, not how many of the (uneven) parts are shaded. Questions that already have equal-sized partitions can lead students into a counting strategy that would not work for the question above. About one-third of the Year 6 students got this and other similar questions correct— answers could be any equivalent fraction of the simplest form (for example, 8/16, 4/8 or 1/2).
About a quarter of students gave incorrect responses to these questions as a result of counting the number of parts irrespective of size. We noted three distinct common errors:
1.&&Writing the number of shaded parts as a whole number (answer 6).
2.&&Counting the number of shaded pieces and placing them over the total number of pieces irrespective of the size of each part (answer 6/11).
3.&&Counting the number of shaded pieces and placing them over the number of unshaded pieces (answer 6/5).
The first error indicated students answered with the number of pieces irrespective of their size. These students may not recognise or know how to construct fractions, and they may need to further explore partitioning and how fractions can be constructed from the parts.
The second and third errors both indicate that students did not consider the size of each of the pieces as important and had a “way” or a system to work out the fraction of a whole region. This may relate to their previous experiences of solving part-whole fraction problems that already had equal-sized parts and did not require them to create their own partitions. Students who constructed the fraction by putting the number of shaded pieces over the number of unshaded pieces set up the fraction as a ratio. A fraction compares a part to the whole, whereas a ratio compares a part to another part. This can be an opportunity to place these similar concepts next to each other and explore the difference between ratio and part-whole fraction concepts.
The above errors involve misconceptions about the size of a part and the nature of wholeness. Equal-sized parts are fundamental to partitioning and to constructing fractional representations of part-whole relationships. Understanding the necessity of equal-sized parts can come from experience with partitioning a range of different shapes or wholes. If students are given problems where the whole shape has already been divided irregularly, it would be hoped that their knowledge of fractions supports them to apply their understanding to the problem. Other students recognised that they could effectively “move and combine” smaller parts to make the larger parts and then name the fraction from these larger parts. These students were working with the “much-ness” of the parts rather than the “many-ness” of the parts. Focusing on “how much” rather than “how many” is an important distinction between thinking about fractions (as rational numbers) and thinking about whole numbers (Anthony & Walshaw, 2003).
Finding the whole … or another part
An important variation on a part-whole fraction question is to give the students a part and ask them what the whole might be, or what another part might be. This type of question can be a good indicator of whether a student has moved from prefraction concepts to a part-whole concept of fractions (Steffe and Olive, 1991).
For example, the level 3 assessment item, Parts and wholes (NM0157), asks students:
Example: 
is 4/5 of a whole shape.
i)&&&&What fraction is  ? ________
? ________
ii)&&&&Draw what the whole shape might look like.
iii)&&&&Draw what 7/5 might look like.
The last question addresses the misconception that students might develop about fractions always being a part of something, and therefore a fraction always being less than one. This misconception is a barrier to students developing a fuller understanding of the part-whole concept (Tzur, 1999, as cited in Olive, 2001).
For the first part of the question, over half of the trial students answered 1/5. Ten percent of students answered 1/4, indicating that they were not interpreting the

as 4/5 but as a whole. For the second and third part, over half the students correctly identified the whole shape and drew 7/5. However, for part three, a number of students drew seven squares and shaded five of them, indicating that they could not reconcile their current understanding with representing an improper fraction. This type of question supports students developing a more robust understanding of the part-whole concept of fractions— including improper fractions.
Another assessment item, Cuisenaires and fractions (NM0134), uses Cuisenaire rods to explore questions that involve finding similar parts to whole. They were encouraged to place the Cuisenaire rods beside each other.
EXAMPLE:
If the black rod is 1/2 then:
i)&&&&What fraction is light green ?_______
ii)&&&&What fraction is red ?_______
iii)&&&&What fraction is blue ?_______

Students in this pilot investigation found that using Cuisenaire rods supported their understanding, and most students could correctly answer many of the questions. Students could use the smaller Cuisenaire pieces to find how many went into a larger one. Many students looked for a unit fraction they could use as a base to build the other fractions. For example:
Dark green is a half (6 whites), so it takes 12 whites to make a whole (each white is 1/12).
Light green is 3 whites (3/12), and red is 2 whites which must be 2/12.
The question students found most difficult was part three, “If the dark green rod is 1/2 then what fraction is blue?” Ultimately this involves finding a smaller unit and combining them together or adding 1/2 and 1/4 (1/2 of 1/2). However, over three-quarters of the 30 Year 5 students solved this problem correctly. Steencken and Maher (2002) explored students’ understandings of fraction ideas using Cuisenaire rods to represent a number of fraction problems. They found that students “built some very important understandings about fractions” (p. 59), including maintaining a consistent whole.
Conclusion
Partitioning and the part-whole concept of fractions are two important fraction concepts amongst many other concepts and personalities that students must eventually explore to develop an understanding of fractions. The fractional thinking concept map on the ARB website describes a number of other concepts, such as Equivalence, Adding and subtracting fractions, Fractions as operators and Fractions and number lines, that all link to a range of assessment items. These concepts and assessment items will be added to as the concept map is further developed in the future.
The assessment items used to illustrate the two fraction concepts in this article represent some key ideas about understanding fractions. Although the items have specific teaching and learning information, developing meaningful learning with fractions in the classroom still depends upon how teachers connect these fraction concepts to their students’ own learning.
References
Anthony, G., & Walshaw, M. (2003, July). Pizza for dinner: How ‘much’ or how ‘many’? Paper presented at the Mathematics Education Research Group Association annual conference, Geelong.
Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best evidence synthesis iteration. Wellington: Ministry of Education.
Baturo, A. R. (2004). Empowering Andrea to help year 5 students construct fraction understanding. In M. Hoines & A. Fugelstad (Eds.), Proceedings of the 28th annual conference of the International Group for the Psychology of Mathematics Education, July 14–18, 2004, Bergen, Norway (Vol. 2, pp. 95–102). Retrieved from: http://www.emis.de/proceedings/PME28/RR/RR170_Baturo.pdf
Behr, M. J., Lesh, R., Post, T., & Silver, E. A. (1983). Rational-number concepts. In R. Lesh & M. Landau (Eds.), Acquisition of mathematics concepts and processes (pp. 91–126). New York: Academic Press.
Chinnappan, M. (2005). Children’s mappings of part-whole construct of fractions. In P. Clarkson et al. (Eds.), Building connections: Theory, research and practice: Proceedings of the annual conference held at RMIT, Melbourne, 7th–9th July, 2005 (pp. 241–248). Sydney: Mathematics Education Research Group of Australia.
Flockton, L., Crooks, T., Smith, J., & Smith, L. F. (2006). National Education Monitoring Report 37, Mathematics: Assessment results 2005. Dunedin: Educational Assessment Research Unit, University of Otago.
Kieren, T. E. (1993). Rational and fractional numbers: From quotient fields to recursive understanding. In T. P. Carpenter, E. Fennema, & T. A. Romberg (Eds.), Rational numbers: An integration of research (pp. 49–84). Hillsdale, NJ: Lawrence Erlbaum.
Kieren, T. E. (1995). Creating spaces for learning fractions. In J. T. Sowder & B. P. Schappelle (Eds.), Providing a foundation for teaching mathematics in the middle grades (pp. 31–45). Albany, NY: State University of New York Press.
Lamon, S. (1999). Teaching fractions and ratios for understanding: Essential content knowledge and instructional strategies for teachers. Mahwah, NJ: Lawrence Erlbaum.
Mack, N. K. (1990). Learning fractions with understanding: Building on informal knowledge. Journal for Research in Mathematics Education, 21, 16–32.
Ministry of Education. (2007). The New Zealand curriculum. Wellington: Learning Media.
Moss, J., & Case, R. (1999). Developing children’s understanding of the rational numbers: A new model and an experimental curriculum. Journal for Research in Mathematics Education, 30(2), 122–147.
Newstead, K., & Murray, H. (1998). Young students’ constructions of fractions. In A. Olivier & K. Newstead (Eds.), Proceedings of the twenty-second international conference for the Psychology of Mathematics Education (Vol. 3, pp. 295– 302). Stellenbosch, South Africa: University of Stellenbosch.
Olive, J. (2001). Connecting partitioning and iterating: A path to improper fractions. In M. van den Heuvel-Panhuizen (Ed.), Proceedings of the 25th Conference of the International Group for the Psychology of Mathematics Education (PME-25) (Vol. 4, pp. 1–8). Utrecht, Netherlands: Freudenthal Institute.
Pothier, Y., & Sawada, D. (1983). Partitioning: The emergence of rational number ideas in young children. Journal for Research in Mathematics Education, 14(4), 307–317.
Smith, J. P. (2002). The development of students’ knowledge of fractions and ratios. In G. Bright & B. Litwiller (Eds.), Making sense of fractions, ratios, and proportions: 2002 yearbook (pp. 3–17). Reston, VA: National Council of Teachers of Mathematics.
Steencken, E. P., & Maher, C. A. (2002). Young children’s growing understanding of fraction ideas. In G. Bright & B. Litwiller (Eds.), Making sense of fractions, ratios, and proportions: 2002 yearbook (pp. 49–60). Reston, VA: National Council of Teachers of Mathematics.
Steffe, L. P. (2002). A new hypothesis concerning children’s fractional knowledge. Journal of Mathematical Behavior, 20, 267–307.
Steffe, L. P., & Olive, J. (1991, May). The problem of fractions in the elementary school. Arithmetic Teacher, 38, 22–24.
Vanhile, L., & Baroody, A. J. (2002). Fraction instruction that fosters multiplicative reasoning. In G. Bright & B. Litwiller (Eds.), Making sense of fractions, ratios, and proportions: 2002 yearbook (pp. 224–236). Reston, VA: National Council of Teachers of Mathematics.
Young-Loveridge, J., Taylor, M., Hāwera, N., & Sharma, S. (2007). Year 7–8 students’ solution strategies for a task involving addition of unlike fractions. In Findings from the Numeracy Development Projects: 2006 (pp. 67–84). Wellington: Ministry of Education.
Notes
&&&&1 The Assessment Resource Banks are an online collection of curriculum-based assessment items in mathematics, English and science: http://arb.nzcer.org.nz
&&&&2 http://arb.nzcer.org.nz/supportmaterials/maths/concept_map_fractions.php
&&&&3 A fraction as a measure is when an interval can be divided into ever-reducing smaller parts (for example, on a number line), such that the detail of the measure gets more detailed (and accurate) as the parts are divided. This relates to the density of fractions as rational numbers (Lamon, 1999). For example, on a number line, between any two rational numbers there are an infinite number of other rational numbers.
JONATHAN FISHER is a researcher and resource developer at the New Zealand Council for Educational Research, specialising in mathematics education.
Email: jonathan.fisher@nzcer.org.nz