Assessing students’ maths self-efficacy and achievement
LINDA BONNE AND ELLIOT LAWES
We describe new PAT: Mathematics assessment items that focus on students’ maths self-efficacy (students’ belief in their ability to correctly solve particular maths problems). In 2017, schools using PAT: Mathematics online will be able to give their students an opportunity to respond to these items to help build a picture of New Zealand students’ maths self-efficacy and achievement.
Relationships between students’ maths self-efficacy and maths achievement have been well-researched overseas. Much less is known about how the relationship plays out over time for different groups of students in Aotearoa New Zealand. We explain why it is important to learn more about this, and introduce a new research project that is doing just that. We also present a collection of practical pedagogical strategies teachers can use to strengthen students’ maths self-efficacy.
Setting the scene
A few weeks into the new school year, a small group of 7 year olds from several classes are brought together for maths lessons that focus on strengthening their knowledge of number. These students have been identified by their teachers as being at risk of not achieving the maths expectations for their year level. Some of them were in similar groups the previous year, and for them, struggling in maths is already a familiar experience. At least half the students seem reluctant to engage with the maths activities presented by the teacher, even though she has deliberately chosen activities that could allow students with a range of understandings to be successful. Indeed, some students seem to expect to encounter difficulty—or to simply fail.
For these students, self-belief is a barrier to learning maths content, and it blocks their progress. More specifically, the students’ maths self-efficacy—their judgments about their own ability to successfully engage in specific maths activities—is probably low. Maths self-efficacy and achievement are related, so it should come as no surprise for these students to have both low maths achievement and low self-efficacy.
So what exactly is “maths self-efficacy” anyway?
Maths self-efficacy is one of a number of beliefs and attitudes that have been linked to New Zealand students’ achievement in maths.1 Self-efficacy can be thought of as part of the key competency, managing self, which is “associated with self-motivation, a ‘can-do’ attitude, and with students seeing themselves as capable learners” (Ministry of Education, 2007, p. 12). One of the leaders in self-efficacy research and theory development, Albert Bandura, described self-efficacy as:
people’s judgments of their capabilities to organize and execute courses of action required to attain designated types of performances. It is concerned not with the skills one has but with judgments of what one can do with whatever skills one possesses. (Bandura, 1986, p. 391)
A key phrase in Bandura’s description is “designated types of performances”. Sometimes researchers describe people’s general confidence in their maths skill as their “maths self-efficacy”. From the Bandura quote, however, we can see that maths self-efficacy is actually a belief about something more specific than maths in general. When we talk about maths self-efficacy in this article, we mean a person’s judgement of their capability to solve particular maths problems. (Later in the article, you will see a example of the questions we are asking students.)
On what basis does a student make maths self-efficacy judgments? Bandura (1997) listed the information sources that shape maths self-efficacy judgments, in order of magnitude of effect.
•The student’s past performances—if they know they’ve successfully solved similar problems in the past, they’re likely to believe they can do this again.
•Observations of their peers—seeing students who they perceive to be similar to themselves succeed or fail will influence their own maths self-efficacy.
•Social persuasion—includes encouragement and feedback from teachers, peers, parents and whānau, especially when the student subsequently experiences success.
•Physiological and emotional cues—signs of anxiety, such as a rapid heartbeat or sweaty palms can undermine a student’s belief that they can succeed at a task.
This is a simplified summary of the information a student will draw on. These various sources will be combined in complex ways, usually below the level of a student’s conscious awareness.
Why is maths self-efficacy important?
A student’s maths self-efficacy will influence how much effort the student exerts, and how long the student is prepared to persevere when adversity or failure is encountered. Therefore a student’s self-efficacy is likely to affect maths achievement.
It should come as no surprise, then, that there is a positive relationship between maths self-efficacy and achievement; as achievement strengthens, this positively influences subsequent self-efficacy, which in turn is associated with improvements in later achievement (Chen, 2003; Pajares & Graham, 1999).
What can teachers do to strengthen students’ maths self-efficacy?
A recent New Zealand study (described in Bonne & Johnston, 2016), based on work by Siegle and McCoach (2007) and Schunk and Hanson (1985), suggested that students’ self-efficacy is likely to be strengthened when:
1.students see someone like them showing the rest of the class their maths work, or explaining how they solved a problem
2.students have strategies for coping when learning is difficult, and when they make mistakes or fail
3.students know what their learning goals are, and understand what they need to do to achieve their goals
4.teachers give students feedback about the progress they are making towards their learning goals, and let them know what they need to do next to help them achieve their goals
5.teachers encourage students to reflect on the role of effort in their learning, and—when appropriate—prompt students to attribute failure to insufficient effort, and encourage them to try harder and persevere when learning is difficult
6.students’ attention is drawn to the specific skills they have developed
7.students are enabled to develop internal standards for evaluating their own outcomes, rather than to rank themselves in comparison to others
8.if a teacher—or a parent—found maths difficult when they were at school, then rather than commiserate with students, they challenge students to improve their maths—expect them to succeed, and give them the support they need to do so.
Teachers—and students’ parents, whānau, and friends—can have a significant impact on a student’s maths self-efficacy. The models a student observes, and the feedback received from others, shape how the student perceives his or her own abilities—in maths and beyond.
And now, introducing some new research …
The literature is clear that maths self-efficacy is an important factor that influences, and is influenced by, maths achievement. However, much about the relationship between achievement and self-efficacy remains unclear. For example, is the relationship between maths self-efficacy and achievement the same for students from different cultural backgrounds? Is that relationship the same for students from different year levels? And how does that relationship change over time?
At the New Zealand Council for Educational Research (NZCER) we are currently conducting research that seeks to answer these questions. Our research is driven by the desire to help teachers to incorporate explicit and practical strategies focused on maths self-efficacy and achievement in their classroom teaching.
Of course, trying to answer the questions above is not as easy as it seems. How do you even measure maths self-efficacy? Over the past few decades, researchers have tried a number of approaches. As Bandura (1997) has suggested, simply asking students how good they think they are at maths in general is not as closely related to their maths achievement as asking students whether they think they could successfully answer a number of specific maths questions.
Our approach at NZCER is to adopt this last idea—with a twist. We will ask students whether they think they could successfully answer a number of specific maths questions for which we know the difficulty on the PAT: Mathematics scale. We will then be able to use a student’s response, together with the difficulty of the PAT: Mathematics questions to which they respond, to measure the student’s maths self-efficacy on the PAT: Mathematics scale. This is a more precise measure than those used in most other maths self-efficacy research.
In the maths self-efficacy questions we’ve developed, students are asked not to solve the problem, but decide whether they think they could. Figure 1 gives an example of what the maths self-efficacy questions looks like.
During 2016, questions such as this have been trialled with over 1,000 students at six schools. The questions are working well and are now ready to go!
In Term 1 2017 we plan to offer every school that uses PAT: Mathematics online the opportunity to participate in this research by choosing the maths self-efficacy option. (In 2017, this will not include the computer adaptive PAT: Mathematics.) This will provide us with maths self-efficacy information and maths achievement information from the same students and we will be able to look at the relationship between these. So what does this mean for students? Before any PAT: Mathematics online test, students will be shown a practice self-efficacy question and will then be asked to respond to four actual self-efficacy questions (different questions go with different tests). Two questions relate to number problems and two questions relate to other strands. These maths self-efficacy questions will have about the same average difficulty as the questions in the actual PAT: Mathematics test. Students who don’t want to participate can simply skip the self-efficacy questions and proceed to the PAT: Mathematics test itself. We think, though, that the self-efficacy assessment will be fun for the students and will take them no more than 5 minutes to complete.
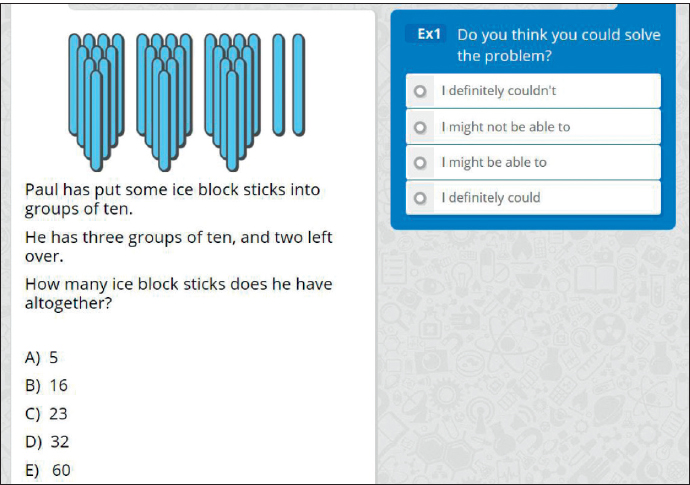
FIGURE 1. MATHS SELF-EFFICACY
We intend to collect this information over the next few years in order to understand how the relationship between maths self-efficacy and achievement changes over time. After that, we will have some new knowledge to share with you, as well as a bank of questions that measure maths self-efficacy. As we carry out this research, we will be sure to let you know how it is going. Watch for more information on this research at: http://www.nzcer.org.nz/research/maths-self-efficacy-and-achievement
Note
References
Bandura, A. (1986). Social foundations of thought and action: A social cognitive theory. Englewood Cliffs, NJ: Prentice-Hall.
Bandura, A., (1997). Self-efficacy: The exercise of control. New York, NY: WH Freeman.
Bonne, L. (2016). New Zealand students’ mathematics-related beliefs and attitudes: Recent evidence. New Zealand Journal of Educational Studies. http://dx.doi.org/10.1007/s40841-016-0035-2
Bonne, L., & Johnston, M. (2016). Students’ beliefs about themselves as mathematics learners. Thinking Skills and Creativity, 20, 17–28. http://dx.doi.org/10.1016/j.tsc.2016.02.001
Chen, P. P. (2003). Exploring the accuracy and predictability of the self-efficacy beliefs of seventh-grade mathematics students. Learning and Individual Differences, 14, 79–92. http://dx.doi.org/10.1016/j.lindif.2003.08.003
Ministry of Education. (2007). The New Zealand curriculum. Wellington: Learning Media.
Pajares, F., & Graham, L. (1999). Self-efficacy, motivation constructs, and mathematics performance of entering middle school students. Contemporary Educational Psychology, 24, 124–139. http://dx.doi.org/10.1006/ceps.1998.0991
Schunk, D. H., & Hanson, A. R. (1985). Peer models: Influence on children’s self-efficacy and achievement. Journal of Educational Psychology, 77, 313–322. http://dx.doi.org/10.1037/0022-0663.77.3.313
Siegle, D., & McCoach, D. B. (2007). Increasing student mathematics self-efficacy through teacher training. Journal of Advanced Academics, 18(2), 278–312.
 Linda Bonne has a background in primary teaching and mathematics education, and is now a senior researcher at the New Zealand Council for Educational Research.
Linda Bonne has a background in primary teaching and mathematics education, and is now a senior researcher at the New Zealand Council for Educational Research.
Email: linda.bonne@nzcer.org.nz
 Elliot Lawes is a psychometrician at the New Zealand Council for Educational Research.
Elliot Lawes is a psychometrician at the New Zealand Council for Educational Research.
Email: elliot.lawes@nzcer.org.nz