Self-regulated learning in mathematics classes

Charles Darr and Jonathan Fisher

If students in mathematics are going to become self-regulated learners, they need to be confronted with opportunities that allow them to represent and examine their own thinking. They also need to be able to observe, critique, and emulate the thinking of others. In our small-scale classroom study into self-regulated learning in mathematics, two elements of instruction stood out as rich sites for students to begin practising self-regulation. The first was the use of models to represent problem situations, and the second, reflective journalling.

In what follows, we take a quick look at self-regulated learning as it pertains to mathematics education, before describing the exploratory study and then examining how models and journalling helped to encourage self-regulating behaviour.

Self-regulated learning and mathematics education

Self-regulated learning happens when students “become masters of their own learning processes” (Zimmerman, 1998, p. 1). Self-regulated learners are actively involved in maximising their opportunities and abilities to learn. They are able to critically evaluate and intentionally alter how their thoughts, attitudes, behaviours, and working environments contribute to learning outcomes. Developing the ability to self-regulate, especially the ability to monitor and control one’s own thinking, is integral to the socio-cultural theories of learning that have influenced mathematics curricula over the last 15 years or so. Traditional learning goals that focused on the mastery of facts and procedures have made way for objectives that emphasise understanding, flexible thinking, communication, and problem solving. Students are now expected to interact with mathematical ideas and problems in an active and constructive way.

Problem solving is the area within mathematics education where the direct application of self-regulatory skills is most apparent. To actively make sense of problem situations, expert problem-solvers employ a fully self-regulated approach: analysing, planning, exploring, and reflecting. In comparison, naive problem solvers are much more haphazard, spending a minimum of time planning or analysing and using “hit and miss” approaches to solve problems (Schoenfeld, 1992), such as attempting to recognise and directly translate certain key words in problems into equivalent mathematical sentences (Pape, Bell, & Yetkin, 2003).

Developing the kinds of pedagogy that lead to self-regulated learning in mathematics learning and problem solving has not proved to be easy. Despite the influence of socio-cultural theories on official curriculum documents, a transmission model of teaching and learning, which emphasises teacher-regulation, often predominates in classrooms.¹

Several researchers have attempted to explore how classroom environments can support the development of self-regulation in mathematics (De Corte, Verschaffel, & Op’t Eynde, 2000; Pape et al., 2003; Schunk, 1996, 1998). In a review of some of this research, De Corte et al. (2000) list three components of instruction that appear to foster self-regulation:

•&&&&realistic and challenging tasks;

•&&&&variation in teaching methods, including teacher modelling, guided practice, small group work, and whole class instruction; and

•&&&&classrooms that foster positive dispositions towards learning mathematics.

The small-scale study

The study reported in this article took the form of a teaching experiment and was conducted with a Year 7 class in a large, mid-decile intermediate school. Carried out at the beginning of the school year, students had come to the intermediate from various contributing schools and had had a wide range of mathematics education experiences. The researchers, in partnership with the classroom teacher, planned and taught 12 lessons based around the area of proportional reasoning over a 4-week period.

Self-regulated learning is highly relevant to proportional reasoning. Becoming a proportional reasoner involves learning to recognise and strategically co-ordinate the elements that make up proportional relationships. A skilled proportional reasoner is an active and self-regulated problem solver, who can analyse a question, choose from a range of strategies, monitor their progress, and reflect on their solutions.

Percentages was chosen as the area of proportional reasoning to focus on. We developed lessons that invited students to apply their intuitive knowledge and understandings about percentages and proportions to meaningful problems. Real and imaginable contexts were developed that we hoped would connect with students’ experiences and motivate them to talk about and examine their problem-solving behaviours. Activities were designed at whole class, group, pair, and individual levels, and time was also provided for students to write about their learning.

To gather some baseline data on students’ proportional reasoning strategies, we designed an interview protocol and a short paper-and-pencil test. The interview protocol was used with the same six students at the beginning and end of the study. All the students took the test at the start and end of the unit. Most of the questions in the test were written to assess elements of proportional reasoning. Some of the problem types we used in the test, however, were not covered in the lessons.

During classroom sessions, one of the researchers co-ordinated the lesson or lesson section while the other videotaped the unfolding events in the classroom. The video camera was often carried around the classroom and used to record interactions with and between students. Data was also collected from several other sources including:

•&&&&artifacts from planning;

•&&&&field notes; and

•&&&&student journals and workbooks.

The initial state of self-regulation

Both the preliminary interviews and the prestudy test suggested that most of the students showed little self-regulation as proportional reasoners. When a well known strategy, such as successive halving, could not be applied to answer a problem quickly, there was little or no further investigation. In many cases, students simply used inappropriate arithmetical operations or provided a guess.

In the following interview transcript, Isabella demonstrates this lack of regulation. Although, to start with, she shows that she can confidently manipulate halves and quarters, as soon as she moves out of this “comfort zone”, Isabella resorts to guessing.

Interviewer: Let’s go back to this one.

How do you know that a quarter of 100 is 25?

Isabella: Because, going back to the question about how many 25s in 100. That’s 4 times 25 is 100. So I just went back to the 4.

Interviewer: And what about this one?

What’s a fifth of 100?

Isabella: What did I say?

Interviewer: I think you said 5.

Isabella: I just looked at one-fifth and sort of guessed it was 5.

There was plenty of evidence, however, suggesting that Isabella had access to knowledge that could have informed her attempt to find a fifth. Later in the interview, she explained that she could form a picture of one-fifth of a hundred, even if she could not calculate it.

Interviewer: What do you think someone’s asking you, when they’re trying to make you get a fifth of something?

Isabella: Well, when someone asks me that…. Go to a pie.

Interviewer: Oh? Show me.

Isabella: [Draws a circle.] This is the pie. If someone asks for a fifth, I’d cut a fifth off…. It’s that [pointing to a fifth section]…. And so—I—that’s 100 [indicates the entire pie] and that’s a fifth [indicates the fifth section].

Interviewer: So how much do you think it would be, do you think?

Isabella: Sixteen.

Interviewer: Sixteen? Something like that?

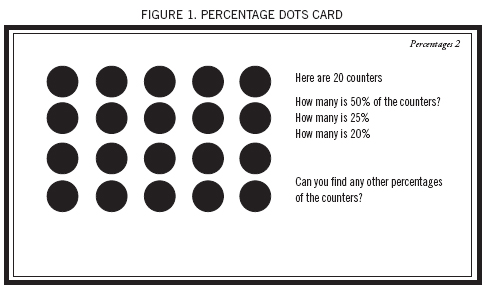
Isabella had other knowledge of fifths too. When she was asked to find 20 percent of the dots in a pattern (see Figure 1), she very quickly demonstrated how the dots could be partitioned into five equally sized groups.

Like Isabella, the majority of the students who were interviewed could draw pictures to help represent a problem or could display knowledge that could have been usefully transferred to a problem situation. Without prompting from the interviewer, however, they were unlikely to do so. If students are not encouraged to report and explain their thinking, much of the knowledge they develop in mathematics classes is in danger of becoming “inert”. (Inert knowledge is knowledge that is available in students’ minds but which they cannot access or apply to new problems and contexts.)

The results of the interviews and pre-study test helped to convince us that we needed to present learning experiences that allowed students to model problem situations and encouraged them to explain and report their thinking. This, we believed, would present opportunities for students to begin to examine and evaluate their own and others’ thinking.

Thinking models

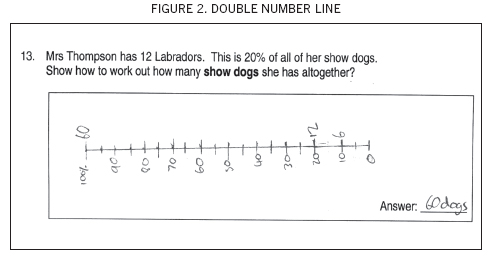
Throughout the teaching experiment, students were introduced to various ways of modelling proportional situations. These included double number lines, geometrical shapes, Cuisenaire rods, and decimal pipes. One of the most successful models was the double number line. This model allows the elements in a proportional relationship to be represented graphically. An example of a double number line is shown in Figure 2.

The double number line was introduced to the students through a series of hands-on activities involving 2-litre milk containers. In the first lesson, pairs of students were given a container and asked to construct a scale that could be used to show both the percentage of milk left and the corresponding number of millilitres. Students very quickly applied successive halving to identify the 50- and 25-percent points on the scale and their corresponding millilitre amounts. Some carried on the halving process to mark in the 12.5 percent point. Many also realised that the scale could be turned upside down and the method reapplied to find out where the 75 percent mark would go.

In the next lesson the students were invited to design a scale for a milk bottle company. To satisfy the company’s design specifications this scale had to be calibrated in 10 percent sections. It also had to be accurate. It soon became obvious to the students that the halving strategy would not be appropriate in this situation. After some discussion, most agreed that the markings could be located by dividing the length of the scale into ten equal intervals. The students then applied their measurement skills to construct the scale and went on to find out how accurate they had been by filling their containers with known amounts of water.

In subsequent discussions, many of the students soon realised that it was now possible to name how many millilitres corresponded to other percentage amounts, such as 35 percent, by finding the halfway points between adjacent multiples of ten percent. The scales were now being used to demonstrate methods to find different percentage amounts.

In creating the scales, the students had become familiar with how to set up and draw a double number line. At this stage, new problems were introduced that were not connected to the milk bottles. New scales, which we now referred to as double number lines, were drawn to solve problems such as “15 percent of 60”. The students were happy to move away from the “concreteness” of the milk-bottle scale to the more generalised double number line. From this point on, regular use was made of double number lines to solve problems and demonstrate thinking. Students used double number lines to explain their solution strategies to their peers and they were frequently referred to by the researchers and the classroom teacher when solutions were modelled to students.

It was also at this point that we were able to observe students engaging in rich discussions about their methods and thinking.

Double number lines often became central in discussions. Alternative solutions were often demonstrated using the same number line, and strategic decisions were justified by appealing to the relationships that had been illustrated.

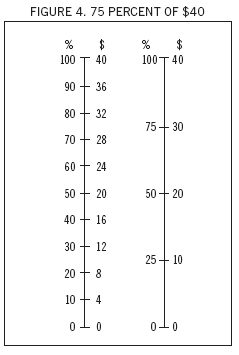
In the transcript below, two students have been working with double number lines to find 75 percent of $40. They have drawn two different number lines (see Figure 4) to solve the problem. In an ensuing discussion with the teacher, the double number lines helped them to explain their methods and make comparisons between them.

Teacher: Can you tell me how you managed to work this out?

Student 1: Well, for this one we divided it into 10 equal bits, and we wanted 75 percent…so we got around about halfway [points to halfway between 70 percent and 80 percent on Line A], which we figured would be exactly in between these two. We took 28 away from 32, which is 4, and then…seeing as we only wanted half, we did 4 divided by 2.

Teacher: You found the difference?

Student 1: Then we went 32 minus 2 equals 30, which is 75 percent.

Teacher: What’s this one set up for?

Student 1: [Pointing to Line B] Well, what happened was we halved 40…which equals 20. And then we halved 20, which is 10, then you plus 20 and 10, which equals 30.

Teacher: Which one [of these two double number lines] do you think was easier— dividing into tens or dividing into halves? Student 1: I think it was that one [pointing to Line B], and then that one was close behind, though.

Teacher: So, if I said to you, say, “What’s 60 percent?”, which one would be best to use?

Student 1: 60 percent? Probably that one [Points to Line A].

Teacher: Okay, and if I said “25 percent?”, which one?

Student 1: That one [points to Line B].

Student 2: That one would be more detailed, though [indicates Line A].

Teacher: So, basically whatever percentage you get asked for, can determine what kind of double number line you make…

In this conversation, the students are able to clearly articulate their thinking. The number line acts as a kind of scaffold that they can literally point to when explaining their methods. Moreover, the students are able to acknowledge two different types of reasoning that lead to the same answer and even discuss which of the two might be more efficient. The students here are thinking about their own thinking (metacognition) and reflecting on their learning, both of which are essential to self-regulated learning.

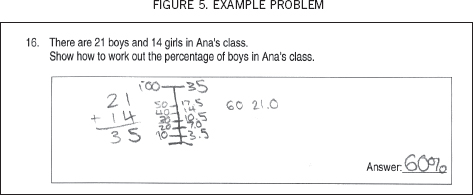
By the end of the series of 12 lessons, many of the students were using the number lines spontaneously to attack questions, check their own working, and represent their thinking. In the post-study test, several students employed number lines to successfully attempt problem types that had not been covered in the lessons. Figure 5 is one example.

In this example the student has identified the 35 students as representing 100 percent of the people in the class. She has then worked out that 10 percent is 3.5 students and built up from there until 21 students (corresponding to 60 percent) has been reached. It is interesting to note that the student was happy to label the number line, but was not concerned about drawing the line to scale.

The double number line played an important role in eliciting and revealing thought, thus allowing the students to engage actively in their mathematics learning and problem solving. In particular, it allowed three important aspects of self-regulated learning to be enacted.

Firstly, it provided a tool for analysis. The double number line allowed students to analyse the components of the problem and develop a visual representation of the proportional relationships involved. In doing so, it lessened some of the cognitive load involved in problem solving and let them concentrate on observing and controlling the problem-solving process. Secondly, it allowed students to explore. Different methods could be recorded or demonstrated on the number lines and the lines used to support reasoning. As students became more familiar with the number lines they recognised strategies that had been applied in similar problems and attempted to apply them in new situations. Thirdly, students also used the number lines to verify their answers. The number lines had to “look right” if the solutions were going to be any good. They also had to convince others.

Models, such as the double number line, invited students to engage in monitoring and controlling their own thinking and helped sustain that engagement. As such, they provided opportunities for students to observe and emulate self-regulating behaviours. In the next section, we look at how involving journalling as a complementary part of the classroom routine provided a structured opportunity for students to reflect on their thinking and mathematics learning.

Journalling

An important phase of self-regulated learning involves reflecting on performance to judge progress and make decisions regarding new goals and altered behaviours. It was decided before the lessons began that a process of journalling could provide significant opportunities for students to examine their thinking and reflect on their learning behaviours.

Journalling in mathematics allows students to write about the experiences, ideas, and feelings involved in their mathematics learning. At its heart, journalling recognises that writing is a means of “knowing what we think”.

…writing can engage all students actively in the deliberate structuring of meaning: it allows learners to go at their own pace; and it provides unique feedback, since writers can immediately read the product of their own thinking on paper.

(Emig, paraphrased by Borasi and

Rose, 1989, p. 384)

Journalling was used in the classroom on six different occasions. Each time, a writing prompt was introduced by one of the researchers to stimulate a writing time lasting for approximately 10 minutes. The prompts developed were generally concerned with the students’ problem-solving behaviour and conceptual development. For instance, one prompt asked students to write a short explanation for a younger child of how to find three-fifths of the squares in a five-by-five grid. In a subsequent session, the students read several of their peers’ responses and an ensuing discussion addressed what made a good mathematical explanation. Students then commented in their journals on the strengths and weaknesses of their own explanations and how they might improve when writing similar explanations in the future.

Writing itself did not present a barrier for the majority of students in the class. Where it did, the task was altered to suit the child. Students were also encouraged to use diagrams and drawings when needed, to illustrate their writing, and were told that the journals would not be assessed for spelling and grammar.

The written feedback by the researchers, who read the journals after each session, promoted further reflection. Students were given time to respond to the feedback, which often asked questions about what they had written or requested them to clarify their thinking or provide further examples. Feedback from the journalling was often used to initiate discussion about learning on a whole class or group basis. Moreover, it helped focus lesson direction and content, often highlighting developing misconceptions and areas of need.

In the example shown in Figure 6, a student has written an explanation of how to divide 70 into 10-percent sections. He has illustrated his method with a double number line. Written feedback from the teacher has resulted in a response in a following lesson. His answer shows that he can think in a flexible manner and is developing increasing sophistication as a proportional reasoner. The journal has provided an opportunity to reflect on his thinking and provided a “window” through which the teacher can observe his increasing range of strategies.

Journalling took time, both to complete in the classroom and for the researchers to read the journals before the next lesson. In a busy classroom, the practice could be hard to sustain. However, it quickly became evident that the process did not have to occur every lesson. We would argue that the benefits to the mathematics programme—and even to writing generally—make this sort of activity very worthwhile.

Conclusion

An important aspect of self-regulated learning in mathematics involves developing an awareness of how one’s own thinking can be used to provide problem-solving options and strategies. However, developing the ability to self-regulate in mathematics learning or as a proportional reasoner does not happen in a vacuum. Supportive classroom environments that nurture the types of thinking and behaviours that support self-regulated learning are critical. In this study we have identified thinking models and reflective journalling as two elements of instruction that do just that. Both of these provided students with opportunities to structure and reflect on their thinking and to observe the thinking of others. When they did this, many demonstrated that they could engage in learning about proportional reasoning in an active way.

The work we have done here represents only a tentative start in exploring how some principles of self-regulated learning might be integrated into mathematics teaching and learning. Overall, we feel that self-regulated learning provides a valuable perspective on instruction that can help promote the kinds of classroom norms that support the development of powerful learning and learners.

References

Borasi, R., & Rose, B. (1989). Journal writing and mathematics instruction. Educational Studies in Mathematics, 20, 347–365.

De Corte, E., Verschaffel, L., & Op ‘t Eynde, P. (2000). Self-regulation: A characteristic and a goal of mathematics education. In M. Boekaerts, P. Pintrich, & M. Zeidner (Eds.), Handbook of self-regulation (pp. 687–722). San Diego: Academic Press.

Pape, S., Bell. C., & Yetkin, I. (2003). Developing mathematical thinking and self-regulated learning: A teaching experiment in a seventh-grade mathematics classroom. Educational Studies in Mathematics, 53, 179–202.

Schoenfeld., A. (1992). Learning to think mathematically: Problem solving, metacognition and sense making in mathematics. In D. A. Grouws (Ed.), Handbook for research on mathematics teaching and learning (pp. 334–370). New York: Macmillan.

Schunk, D. (1996). Goal and self-evaluative influences during children’s cognitive skill learning. American Educational Research Journal, 33(2), 359–382.

Schunk, D. (1998). Teaching elementary students to self-regulate practice of mathematical skills with modeling. In D. Schunk & B. Zimmerman (Eds.), Self-regulated learning: From teaching to self-reflective practice (pp. 137–159). New York: Guilford Press.

Zimmerman, B. (1998). Developing self-fulfilling cycles of academic regulation: An analysis of exemplary instructional models. In D. Schunk & B. Zimmerman (Eds.), Self-regulated learning: From teaching to self-reflective practice (pp. 1–19). New York: Guilford Press.

Footnotes

1&&&&Pape et al. (2003) argue, moreover, that at times a lack of explicit teacher guidelines on how to enact socio-cultural pedagogies also hinders the development of self-regulated learning. They advocate programmes of instruction that combine socio-cultural ideas with the principles of self-regulated learning.