ESTIMATION EXPOSED

Alex Neill

This article reports on a research study that was designed to explore how instruction could help students develop a richer understanding of estimation and a wider range of strategies. The students started with a fairly limited understanding of estimation, often equating it with rounding. They quickly developed new skills and a new awareness of how estimation could enrich their mathematical skills.

Estimation

Why is estimation important?

Estimation is a skill that we all use in our daily lives. Reys and Reys (1990, p. 22) say, “Do you estimate? Of course you do. Everyone estimates”. Every time you do an exact calculation, you need to ask “Is my answer sensible?” This requires estimation. When shopping, the canny customer estimates the approximate size of the bill, or uses “quick-and-close-enough” mental computations to work out the best value for money. It is also useful to know how to estimate because some problems do not have an exact answer.

Encouraging estimation skills enriches students’ understandings of mathematics. Good estimation skills go hand in hand with good number sense and mathematical thinking. Sowder (1992, p. 381) draws attention to the interaction between number sense and estimation. She states that “Good estimators are flexible in their thinking, and they use a variety of strategies. They demonstrate a deep understanding of numbers and operations and they continually draw upon that understanding”.

A study by Knight, Arnold, Carter, Kelly, and Thornley (1994), found that estimation was the second most common use of mathematics in the workplace, with about 85 percent of people using it. Eight of the nine students in our study said that they use estimation. The most common context (identified by six of the nine students) was shopping, where amounts of money are estimated. Food catering, time, games, and mathematics were the other uses the nine students mentioned.

There is evidence that New Zealand students are not particularly strong in estimation skills. The most recent NEMP report (Crooks & Flockton, 2002, p. 3) found that “students at both levels (Year 4 and 8) scored poorly in tasks involving estimation”. Similarly, an analysis of the Assessment Resource Banks (ARBs) mathematics results revealed that students are weaker in estimation than in most other number strategies (Neill, 2003).

This weakness in estimation is despite the current mathematics curriculum (Ministry of Education, 1992, p. 31) giving a strong emphasis to the subject, stating that students should “develop the ability to estimate and to make approximations, and to be alert to the reasonableness of results and measurements”. Discussions surrounding the development of the new curriculum have identified that estimation should continue to be an important facet in the teaching of mathematics.

The Numeracy Project encourages the use of a range of strategies for computation (see Ministry of Education, 2004, pp. 9–11). Many of the strategies that are introduced for exact computation can be applied at least equally well to estimation.

Unfortunately, estimation skills in schools settings have often been reduced to techniques based only on rounding strategies. Although rounding is a powerful tool for estimation, other excellent methods are also available. For instance, the front-end method uses only the first digit of each number. It is extremely easy to use and makes it very easy to update an initial estimate to a more accurate one.

There are several forms of estimation:

•&&&estimating the numbers in sets of distinct objects (referred to as numerosity);

•&&&estimating the sizes of measurements such as height, weight, and area (measurement estimation);

•&&&estimating answers to computational problems (computational estimation); and

•&&&estimation in statistics.

This article focuses on computational estimation.

What is computational estimation?

Computational estimation involves being able to identify, quickly and easily, a number that is close enough to the exact answer to an arithmetic problem to be useful. It involves using simplified calculations that usually can be done mentally. The forms of these computations vary and depend on the creativity and lateral thinking of the estimator. Essentially, any strategy that gives a reasonable answer is acceptable.

Computational estimation is:

•&&&using some computation;

•&&&using easy mental strategies;

•&&&using number sense;

•&&&using a variety of strategies; and

•&&&getting close to the exact answer.

It is not:

•&&&just a guess;

•&&&doing hand calculations;

•&&&using a calculator; or

•&&&exact.

Using estimation strategies

People who are adept at estimation are able to apply a wide range of strategies to find a useful answer with a minimum of calculation. One of these strategies is to use rounding. For instance, when estimating the problem below, rounding the numbers to the nearest power of 10 can provide a quick estimate.

57 × 62 is about 60 × 60 However, rounding is only one method and in some situations, it’s not the most effective way to estimate. For example:

228 ÷ 7 could be estimated by working out 230 ÷ 7 (rounding to the nearest 10) or 200 ÷ 7 (rounding to the nearest 100). However, both of these are just as difficult as the original problem.

A better strategy might be to use “nice numbers”. A nice number strategy involves exploiting well-known relationships between numbers to reformulate the problem into a similar, but easier question.

For instance, 228 ÷ 7 could be reformulated as 210 ÷ 7.

There are many other strategies that can be used to produce useful estimates. Some of these involve using only the first digit of the numbers (front-end estimation), making adjustments before or after an initial calculation (compensation), or even changing the actual mathematical structure of the problem (translating). A successful estimator is aware of these different strategies and able to exploit them. They don’t just rely on rounding.

The research project

This project aimed to enhance the estimation skills of a group of intermediate school students. Nine Year 8 students were selected, all of whom had the prerequisite skills and attitudes for being good estimators. Sowder (1992) and Reys and Reys (1998) comment on the need for a good number sense built on basic skills and understandings, as well as the ability to handle big numbers.

Skills of good estimators include

•&&&having good basic fact knowledge;

•&&&being able to do mental computation;

•&&&understanding operations;

•&&&having place-value knowledge;

•&&&having good number sense; and

•&&&being able to work with powers of 10, especially in multiplication or division.

Attitudes of good estimators include

•&&&being confident and positive about mathematics;

•&&&recognising the usefulness of estimation;

•&&&being willing to accept a range of strategies;

•&&&being willing to accept a range of estimated values; and

•&&&being a versatile thinker.

Method

Each student was individually interviewed both before and after a series of lessons. They were asked a variety of questions about estimation, such as how they defined it, when they used it, and how confident they were as estimators. They were also asked to perform a number of estimation tasks, some of which were common to both interviews.

The group then undertook a series of eight lessons on estimation strategies. These were centred around active learning experiences and extensive discussion on students’ estimation strategies. The lessons involved a carefully selected series of tasks. Some of these tasks encouraged a wide range of possible strategies, so that students could compare each other’s methods. Others were designed to focus attention on a particular strategy, to ensure that it could be added to each student’s repertoire. Students recorded the strategies they used for each task on a worksheet. After each lesson, the students kept a journal where they reflected on their learning.

To aid in discussion, the students sat in three separate groups, with three students in each group. Many different estimation tasks were given. Most often students started these tasks individually. They would then discuss in their small groups the strategies that they used. Each group would then share some of their methods with the other groups. This allowed the students to model to each other and to observe a range of different strategies.

The following findings are based on two video interviews for each student, the individual worksheets, and the reflective journals.

Results

Expansion of estimation strategies

After the series of lessons, students demonstrated a far larger number of estimation strategies. On the estimation problems given before the lessons, the nine students used between one and four different estimation strategies (with an average of nearly three strategies per student). After the lessons, students were using between four and seven distinct strategies (with an average of nearly six strategies per student). In the final interview, all students acknowledged that they had learnt new strategies and were able to name up to four of them.

Broadening of mathematical understanding

There was evidence that students were beginning to show growth in their mathematical understandings, both in the comments they made and in the sophistication of their estimation. Students were beginning to unpack problems and make strategic decisions. An example of this was seen when the following question was asked:

If fish cost $9.35 each, how many whole fish could you buy for $72?

All the students used estimation rather than exact calculation in both the pre-study interview and the post-study interview. Before the lessons, only two out of the nine students gave the correct answer (seven fish) while the rest said they could buy eight. However, after the lessons, seven students were correct. The students were now recognising that they needed to round $9.35 up to $10, or make a final compensation to allow for the extra 35 cents.

Here are some comments some students made, indicating their self-recognition of the improvements they had made or needed to make in mathematics or estimation.

Student E: I learnt an easy way to do 100 × 100. I switched one zero so it looked like 10 × 1000 = 10 000. That was my “Aha” moment…. I would like to know more about (10¹⁰)².

Student G: I think I got better at calculating for some strange, strange reason. I find it really hard to stop myself calculating but not estimating, because I never used to know how.

Students’ definition of estimation

Students showed an increasing awareness of the power and scope of estimation. In the pre-study interview, five of the nine students strongly linked estimating with rounding. After the lessons, no student placed an emphasis on rounding in this same way, all preferring to mention a variety of ways to estimate. There was also a much greater emphasis on defining estimation as quick and easy. Student H provides an example of this new awareness of estimation. Here is what Student H said before the lessons,

Estimation is just guessing… [prompt] rounding it up or down. Afterwards, student H stated:

It’s like a way of quickly solving problems, and it’s just like guessing… [prompt] using all kind of ways to estimate.

Recognising estimation

The students’ more sophisticated awareness of estimation led them to recognise instances of appropriate estimation readily. In both interviews, students were asked to identify which of a set of strategies involved estimation and which did not (see Figure 1).

All the students could readily identify that Gabby was not estimating but calculating exactly. They were equally confident that Leslie was estimating, as the students were all very comfortable with rounding before the study began. Indeed, they particularly liked his method.

Responses to what Sam did varied. In the pre-study interview, only two said he wasn’t estimating, but seven students thought he was. There were some reservations as to how accurate his estimation was. In the post-study interview, all students were happy that he was estimating.

There were problems when it came to John and Isaac, because the students equated estimation with rounding. Before the series of lessons, four students thought that perhaps Isacc was estimating, even though he had clearly calculated. Here are some pre-study interview responses for what Isaac did, showing the range of responses to rounding after an exact computation.

Student H: Yes [he’s estimating] …because he’s rounding.

Student B: Huh [laughs] …so he just [calculated it] and rounded them, eh? I’m not sure. I think it is sort of, but…

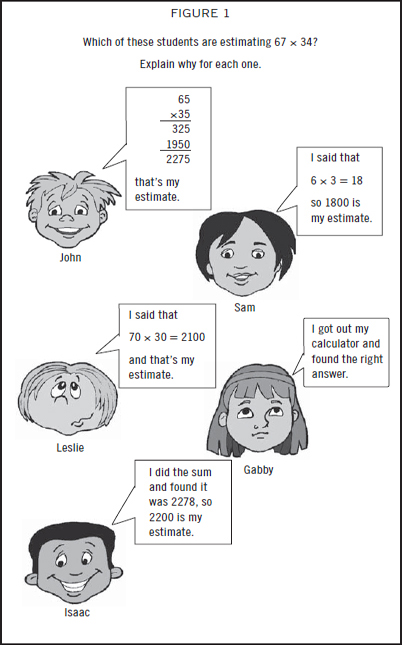
Student A: No [he’s not estimating]. He got the sum and found out what it was and then he made it so it looked like an estimate.

The issues were slightly different for John. Here it is important to recognise that for John to be successfully estimating, he needs to round in a way that makes mental computation easier. Most students would not find this any easier than the original question. So John here is rounding, but because he is not rounding sensibly, he is not estimating successfully. Even after the lessons on estimation, seven of the nine thought John was estimating, although five of these did express some reservations. A range of responses were given:

Student H: Yes [he’s estimating] because he’s rounding it.

Student E: No [he’s not estimating] because he is…oh he is [estimating] but it’s a long way of estimating. [He] might as well get what the answer is.

Student G: He’s not estimating the way I see it. He’s just calculated it.

Students attitudes to estimation

Students also developed more positive attitudes towards estimation. When asked at the final interview, all but two of the nine had become more positive about estimation. Common themes were that they felt more confident about estimating, knew more strategies, found it easier, and were quicker at it.

Student B: I’m a lot more confident when I do it and it’s a bit more easy for me. I’m quicker.”

Student C: I am getting better at adjusting my estimates. I have definitely got better at estimation since the beginning of the lessons.

Student E: I think now [estimation] is more important, and I’ve learnt some new ways and it’s a lot quicker.

Students learnt strategies from each other

The sharing and discussion focus of the lessons meant that students learnt new ideas from each other. Some comments that they made indicate this, for example:

Student A: I liked [students G and M’s] method…. I liked how [E] mixed front-end and rounding.

Student C: I learnt more about adding zeros on…as [A] said.

Student E: I discovered how the other people in my group estimate….

I learnt that everyone has a wide range of strategies.

Discussion

After the series of teaching sessions, the students had a broader range of estimation strategies at their fingertips. They were, on the whole, more confident and positive towards estimation. This suggests that focused lessons on estimation are effective. Developing estimation awareness is a long-term process. While this project delivered an intense programme in a short timeframe, it may be more realistic for teachers to include a little estimation at a time as a regular part of their mathematics programme.

There was a spin-off into the students’ wider mathematical understandings as well. One specific area that the students consistently commented on and wished to make further progress in was working with large numbers, especially with multiplication and division by powers of 10. This was revisited several times, beginning with drawing up a table showing multiplication results for powers of 10 (we called it the “new 10-times table”), and moving on to the law of indices. Many students had rightly perceived that this is a vital estimation skill. If an estimate is in the wrong order of magnitude (for example, ten times too big or too small) it is of little use.

The issue of rounding was still a problem area. Some students thought that they were estimating if they did any rounding. In reality they need to understand that if a number is rounded, the rounding must substantially simplify the problem. Rounding has probably been over emphasised up to now, and a broader view of estimation needs to be taken.

The other behaviour that was commonly observed in the study was students’ dependency on exact computational methods. On a number of occasions, students checked their estimates with exact calculations. They need to change this mindset and instead start to use estimation to check whether exact calculations are sensible.

Implications for teaching and learning

Suggestions for teaching computational estimation

Some pointers for introducing and teaching estimation follow. These have been collated from both the literature and the experience gained in the eight teaching sessions:

•&&&Discuss what estimation is. Contrast computation and estimation.

•&&&Use real examples

•&&&Discuss why estimation is important. Use situations where an estimate is acceptable or essential.

•&&&Find out where students use estimation and what they know about it.

•&&&Value the role of estimation.

•&&&Use the language of estimation.

•&&&Accept a range of estimates.

•&&&Discuss a range of strategies.

•&&&Encourage students to share strategies.

•&&&Expand students’ repertoires of estimation strategies.

•&&&Use examples that aren’t too hard or too easy.

•&&&Do a little of it often.

•&&&Emphasise mental strategies.

•&&&To encourage estimation, occasionally limit the time available to students.

•&&&Link estimation with assessing the reasonableness of exact calculations.

Language of estimation

When doing estimation, use both the formal and the informal language of estimation. Formal terms such as front-end, rounding, compensation, and averaging should be used regularly so that they become embedded in students’ mathematics vocabulary.

The informal language of estimation should also be used. Use words and phrases like about, roughly, educated guess, good guess, guesstimate, close to, thereabouts, something like, not far from, more or less, and is near enough to.

Avoid round about, as it reinforces the very common misconception that estimation is merely rounding, rather than a rich range of strategies.

Expanding students’ repertoires of estimation strategies

Figure 2 illustrates a simple sequence that was used in the project for introducing a specific estimation strategy that students might not have previously seen. A number of ARB resources have this structure (for example, NM1200 and NM1210).

Conclusion

While there is general agreement that estimation is important, many students either struggle with it, or have a very limited view of it. Many students (and teachers), equate estimation with rounding. By arming them with a range of strategies, you can empower students to become increasingly effective estimators, choosing and refining strategies to meet each individual situation they meet.

Finding out more about estimation

Many of the resources that were developed from this project are now available on the ARBs. As well as this, the ARBs have a central framework statement that gives background information on computational estimation and has links to many estimation resources.

Using the ARBs

1.&&Go to the New Zealand Council for Educational Research website (www.nzcer.org.nz).

2.&&Click on the Assessment Resource Banks button.

3.&&Click the Maths button. If you need a password, click on Register to receive a password under the “About the ARBs” menu and Accessing the ARBs.

4.&&Click on Big ideas under the Maths button

5.&&Click on computational estimation information. You will find many estimation assessment tasks linked to this document.

References

Crooks, T., & Flockton, L. (2002). Mathematics Assessment results. NEMP monitoring report 23. Dunedin: Educational Assessment Research Unit.

Knight, G., Arnold, G., Carter, M., Kelly, P., & Thornley, G. (1994). The mathematical needs of school leavers. set: Research Information for Teachers, 1, item 5.

Ministry of Education. (1992). Mathematics in the New Zealand curriculum. Wellington: Ministry of Education.

Ministry of Education. (2004). Book 1: The Number Framework. Wellington: Ministry of Education.

Neill, A. (2003, July). So what’s hard and what’s easy: An analysis of difficulties of Assessment Resource Bank questions in the Number strand. Eighth New Zealand Association of Mathematics Teachers Conference, Hamilton, New Zealand.

Reys, B. & Reys, R. (1990). Estimation—direction from the standard. Arithmetic Teacher, 37 (7), 22–25.

Reys, B., & Reys, R. (1998). Computation in the elementary curriculum: Shifting the emphasis. Teaching Children Mathematics, 5(4), 236.

Sowder, J. (1992). Estimation and number sense. In Grouws, D. (Ed.) Handbook for research on mathematics teaching and learning (pp. 371– 389). New York: Macmillan.